FUNCIONES TIPOS

Funciones de potencia

Una función de la forma f(x) = x^a , donde a es constante se llama función potencia. Se consideran varios casos.

I. a = n, donde n es un entero positivio.

II. a = 1/n, donde n es un entero positivo.

f(x) = x^1/n = ⁿ√x

III. a = -1

Función reciproca f(x) = x^-1 = 1/x

Función racional

Una función racional f es una razón de dos polinomios

f(x) = P(x)/Q(x)

Funciones algebraicas

Si una función puede construirse usando operaciones algebraicas (suma, resta, multiplicación, división, y extracción de raíz) a partir de polinomios se le llama función algebraica. Cualquier función racional automáticamente es una función algebraica.

Funciones trigonométricas

Son funciones que relacionan los lados del triángulo rectángulo con los ángulos.

Seno, coseno, tangente, secante, cosecante.

Funciones exponenciales

Las funciones exponenciales son las funciones de la forma f(x) = a^x , donde la base a es una constante positiva.

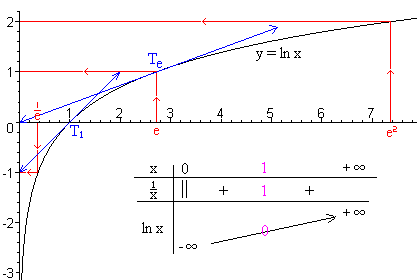
Funciones logarítmica

Las funciones logarítmicas f(x) = log_a x, donde la base a es una constante positiva, son las inversas de las funciones exponenciales.

Ley de los exponentes

Si a y b son números positivos y x y y con cualquier número real, entonces

1. a^{x + y} = a^xa^y          2. a^{x – y} = a^x/a^y       3. (a^x)^y  = a^xy       4. (ab)^x  = a^xb^x